Законы умножения
Содержание
3 закона ключевых закона
В математике существует несколько видов законов умножения, которые необходимо неукоснительно соблюдать:
- Переместительный или коммуникативный закон: b × а = а × b.
- Сочетательный или ассоциативный закон: а × (b × c) = а × b × c.
- Распределительный или дистрибутивный закон, относительно сложения: аd + bd + cd = (а + b + c) × d.
Рассмотрим эти законы более подробно.
Переместительный закон умножения
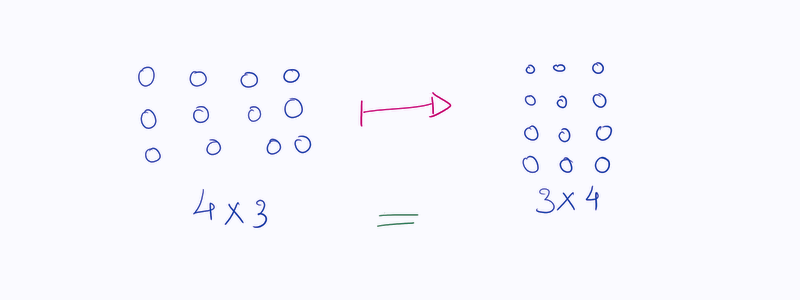
Переместительный закон умножения говорит, что от перемены мест множителей произведение не меняется.
Другими словами, если множитель и множимое поменять местами, то их произведение останется таким же и никак не поменяется. В общем виде переместительное свойство умножения будет выглядеть следующим образом:
a × b = b × a
Давайте проверим на примере, действительно ли это так и есть?
Умножим сначала 5×2, а потом, наоборот, 2×5:
5 × 2 = 10
2 × 5 = 10
В итоге, в том и в другом случае мы получаем один ответ 10 — поэтому между выражениями 5×2 и 2×5 мы можем смело поставить = (знак равенства).
5 × 2 = 2 × 5
10 = 10
В чем заключается переместительное свойство умножения?
Переместительное свойство по-другому называется коммутативное, commutative – то есть то, что может меняться (лат.)
Поэтому, когда мы меняем в действиях порядок сомножителей, то произведение при этом никак не будет меняться.
Существует коммутативность умножения, когда при перестановке сомножителей произведение не меняется.
Также существует коммутативность сложения, когда от перестановки двух слагаемых сумма тоже никак не будет меняться.
Сочетательный закон умножения
Сочетательный закон умножения по-другому называется ассоциативным, association – то есть то, что соединяется (лат).
Сочетательный закон умножения говорит о том, что для того, чтобы умножить произведение двух чисел на какое-то третье число, то первое число можно умножить на произведение второго и третьего чисел.
Умножение числа a на произведение из чисел b и c будет равносильным умножению произведения чисел a и b на число c.
Для примера приведем простую формулировку в буквенном виде:
a × (b × c) = (a × b) × c
a, b, c здесь будут любыми натуральными числами.
Сочетательный закон, как правило, работает для трех и более натуральных чисел.
Разберем еще один полезный и нужный закон в математике.
Сочетательный закон умножения:
Если наше выражение будет состоять из нескольких сомножителей, то их произведение не будет зависеть от порядка действий. Другими словами, вы можете умножать числа абсолютно в любом порядке — как вам больше нравится - так и умножайте.
Например, возьмем такое выражение:
2 × 3 × 4
Его можно вычислить в любом порядке. Для начала давайте перемножим между собой числа два и три, а затем полученный результат умножим на 4:
2 × 3 = 6
6 × 4 = 24
2 × 3 × 4 = 24
А теперь попробуем это действие решить по-другому:
Сначала перемножим числа три и четыре, а затем результат умножим на два:
3 × 4 = 12
2 × 12 = 24
2 × 3 × 4 = 24
Ответ будет таким же.
Это говорит о том, что между выражениями (2 × 3) × 4 и 2 × (3 × 4) мы можем поставить = (знак равенства), так как эти выражения по своему значению между собой абсолютно равны.
(2 × 3) × 4 = 2 × (3 × 4)
6 × 4 = 2 × 12
24 = 24
Для a, b и c (любых натуральных чисел) будет верным такое равенство:
a × b × с = (a × b) × с = a × (b × с).
Например, нам необходимо вычислить: 5 × 6 × 7 × 8.
Метод решения:
Поскольку данное выражение мы можем вычислять в любом порядке, то давайте вычислим его слева направо:
5 × 6 = 30
30 × 7 = 210
210 × 8 = 1680
5 × 6 × 7 × 8 = 1680
Распределительный закон умножения
Распределительный закон умножения гласит:
- Для того, чтобы одно число умножить на сумму чисел, нам нужно это число сначала отдельно умножить на каждое слагаемое и после этого сложить все полученные произведения.
- Для того, чтобы сумму чисел умножить на число, необходимо отдельно каждое слагаемое умножить на число, после чего все полученные произведения необходимо сложить.
Другими словами, при помощи этого распределительного закона умножения можно умножить как сумму на число, так и любое число на сумму.
Как отразить распределительный закон умножения с помощью переменных?
(a + b) × c = a × c + b × c
Выражение, находящееся в скобках (a + b) — называется множимым.
А переменная с в данном случае будет являться множителем, поскольку они соединены между собой знаком умножения.
Давайте рассмотрим следующий пример: (3 + 5) × 2.
В первую очередь мы будем выполнять действие в скобках: (3 + 5) = 8.
В основном выражении (3 + 5) × 2 нам необходимо заменить выражение в скобках на цифру восемь: 8 × 2 = 16.
Мы получаем в ответе «16».
Этот же пример мы можем решить с помощью распределительного закона умножения. Для этого мы возьмем каждое слагаемое в скобках и умножим его на два, а потом сложим между собой полученные результаты:
(3 + 5) × 2 = 3 × 2 + 5 × 2
3 × 2 = 6
5 × 2 = 10
6 + 10 = 16
И здесь мы понимаем, что по правилу переместительного закона умножения от перемены мест множителя и множимого само произведение меняться не будет.
Если, например поменять местами множимое (a + b) и множитель c, то мы получим выражение c × (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). И здесь, для этого действия мы можем пользоваться распределительным законом умножения.
Мы будем умножать переменную на каждое слагаемое в скобках:
c × (a + b) = c × a + c × b
Пример № 1
Нам нужно решить: 5 × (3 + 2).
Как будет выглядеть решение?
Мы умножим цифру пять на каждое слагаемое, которое находится в скобках, по очереди и после этого сложим полученные результаты:
5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25
В ответе получаем: 25
Пример № 2
Попробуем найти значение выражения: 2 × (5 + 2).
Как будем решать?
Возьмем цифру два и умножим ее на каждое слагаемое в скобках по очереди, после чего полученные результаты сложим вместе:
2 × (5 + 2) = 2 × 5 + 2 × 2 = 10 + 4 = 14.
В ответе получаем: 4.
Если в действии в скобках будет не сумма, а разность, то сначала будем умножать множимое на каждое число, которое находится в скобках. А после этого возьмем первое полученное число и вычтем из него второе число.
Пример № 3
Будем решать: 4 × (6 − 2).
Порядок решения:
Умножаем цифру четыре на каждое число, которое находится в скобках. И после этого из полученного первого числа будем отнимать второе число:
4 × (6 − 2) = 4 × 6 − 4 × 2 = 24 − 8 = 16
В ответе получим: 16.