Виды таблиц умножения

Существует множество видов таблиц умножения. Самые старые из известных таблиц умножения использовались вавилонянами еще около 4000 лет назад. С тех пор таблицы умножения менялись, совершенствовались, переосмысливались. И сегодня это целый пласт знаний и пособий.

В этой статье мы подробно разберем самые выдающиеся виды таблиц умножения и расскажем об их особенностях. Но эта информация будет не просто интересной, а еще и полезной с практической точки зрения, ведь какие-то приемы и методы умножения вы сможете использовать сами.

Содержание:

• Китайская таблица умножения
• Таблица умножения и деления
• Древняя таблица умножения на фрагментах бамбуковых полосок
• Таблица на костях Напьера
• Таблица Пифагора
• Древнерусское умножение
• Таблица сокращенного умножения
• Умножение на пальцах
• Пирамида умножения
• Арийское умножение
• Ведический квадрат
• Китайское умножение
• Японское умножение
• Умножение степеней
• Умножение дробей
• Сокращённое умножение
• Умножение в столбик

⛩ Китайская таблица умножения

Китайская таблица умножения была известна еще в период примерно с 770 по 476 (некоторые полагают, что по 403) годы до н.э., что относится к весенне-осеннему периоду в истории Китая. Наиболее же достоверные источники указывают на конец 3 века до н.э., что соответствует династии Цинь.

Сама же таблица является одним из основных условий для использования стержневого исчисления, позволяющего умножать, делить, извлекать корни и решать уравнения с основой на десятичную систему исчисления. Составляет эту таблицу 81 член, а в древности она начиналась с 9 х 9. Поэтому, кстати, нередко ее называют «таблицей девять-девять» или и вовсе просто «девять-девять».

Китайский историк и поэт Ван Говэй считал, что таблица начиналась с девяти, т.к. в древние времена в Китае «поклонялись» девятке. Из таблицы можно было узнать, что «девять девяток дают восемьдесят один, восемь девяток дают семьдесят два, семь девяток порождают шестьдесят три» и т.д.

А еще китайская таблица умножения известна как стихотворение (или песня) «Девять-девять». Таблицу составляют 81 строка и 4 или 5 китайских иероглифов в каждой из строк, что создает постоянный стихотворный размер, отчего таблица и выглядит как стих:

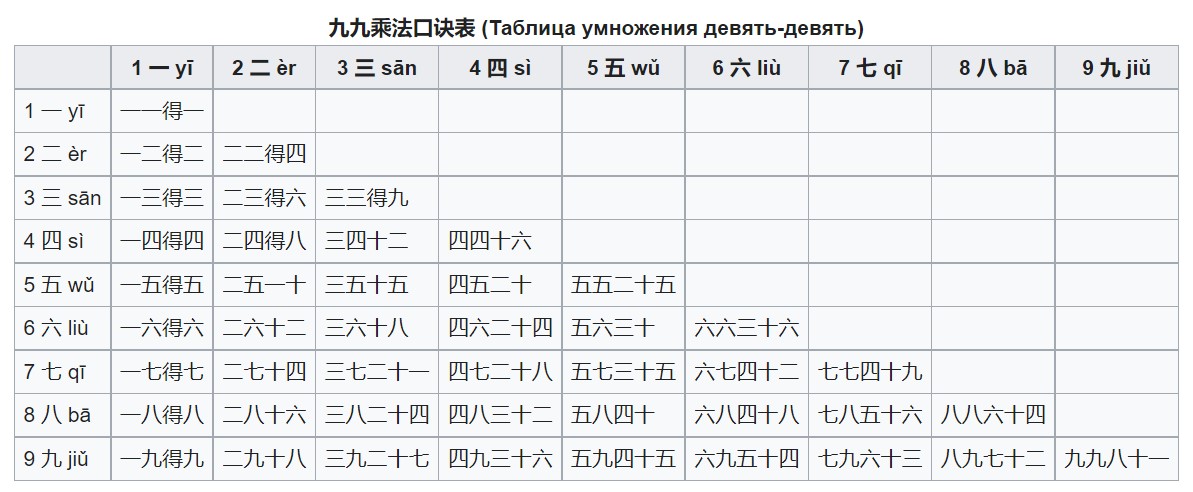
Существует также и сокращенная версия китайской таблицы умножения – в нее входят всего 45 предложений, потому что есть повторяющиеся строки (например, «девять восьмерок порождают семьдесят два» и «восемь девяток порождают семьдесят два»), которые нет смысла учить повторно.

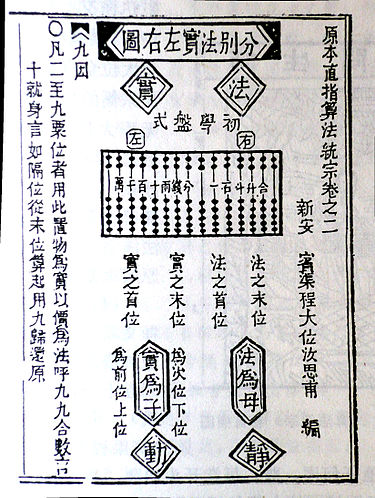
Кроме того, на «Девять-девять» ссылаются в своих произведениях многие китайские классики, такие как Чжоуби Суаньцзин, Гуань Цзы, Фу Си, Ся Хоуян, Сун Хун Чжай, Сун Ян Хуэй, Чжу Шицзе и другие. Вот в таком виде, например, можно встретить таблицу в одной из древних китайских книг:

Сам факт существования китайской таблицы умножения говорит о том, что десятичная система появилась очень давно и была очень востребована, иначе была бы нужна гораздо большая таблица умножения с членами, которые выходят за рамки 9 х 9. Интересно также то, что ученики начальных классов китайских школ даже сегодня должны запоминать именно эту таблицу.

Таблица ✖ умножения и деления ➗

Как мы знаем, умножение является математическим действием сложения одинаковых слагаемых, например, 5 + 5 + 5 + 5 + 5 = 25. Но вместо таких долгих вычислений намного проще оперировать 5 х 5 = 25.

Скорее всего, это понимали уже в древности, а чтобы каждый раз не придумывать новые формулы, однажды составили таблицу умножения, которую можно применять всем людям на протяжении всей жизни. Современная таблица умножения выглядит так:

Однако есть и еще одно важное математическое действие. Оно обратно умножению и называется делением. Деление – это последовательное вычитание одинаковых чисел, т.е. 25 : 5 = 5. Но и здесь оказалось нужным и полезным привести процесс деления простых чисел к конкретной системе.

Так, со временем появилась таблица деления. Заметим, что она пользуется намного меньшей популярностью, чем таблица умножения, но это ни в коей мере не умаляет ее достоинств и пользы. И современная таблица деления выглядит так:

Действие умножения тесно связано с делением, и гораздо лучше назубок знать не только результат перемножения конкретных чисел, но и результат их деления, ведь в жизни нам часто приходится не только умножать, но и делить.

Поэтому педагоги и преподаватели математики рекомендуют осваивать сразу две таблицы. Впрочем, если вы знаете, сколько будет пятью пять, вы так же быстро сможете ответить, сколько будет и наоборот. Однако помочь освоить своему ребенку еще и таблицу деления лишним не будет в любом случае.

🎋 Древняя таблица умножения на фрагментах бамбуковых полосок

В недалеком прошлом самыми древними китайскими десятичными таблицами считались упомянутые нами в самом начале записи с короткими предложениями. Но не так давно Университет Цинхуа в Пекине получил в дар 2500 бамбуковых полосок, на которых впоследствии обнаружили десятичную таблицу умножения:

Исследуя их, специалисты смогли датировать их 305 годом до н.э., и сейчас они считаются древнейшим доказательством существования таблицы умножения с основанием на 10.

Каждая бамбуковая полоска составляет от 7 до 13 мм в ширину и около 50 см в длину. При этом 21-я полоска отличается от остальных – на ней изображены лишь цифры. Расположив полоски правильно, можно получить матричную структуру. В верхнем столбце находятся 19 цифр, начиная 0,5 и заканчивая 90.

Записи на пересечениях строк и столбцов, как и в таблице, которую все мы знаем сегодня и пример которой привели выше, – это результаты умножения чисел. Но эта таблица позволяет умножать как целые числа, так и числа от 0,5 до 99,5.

Исследователи полагают, что данная таблица помогала чиновникам того времени рассчитывать площадь поверхности земли, урожайность культур и налоги, а также вычислять квадратные корни. Очевидно, что уже в древности людям требовалось решать задачи, сходные с современными, но прямых доказательств этому, конечно же, нет.

🗿 Таблица на костях Напьера

Таблица на костях Напьера, также называемая просто «костями Напьера», – это счетный прибор, изобретенный в 17 веке шотландским математиком Джоном Напьером (Непером). Прибор управляется вручную и позволяет вычислять частные и произведения заданных чисел. Он напоминает настольную игру с ободками и стержнями, которые помещаются в ободки, где написаны числа:

Существует несколько видов костей Напьера:

• Индексная кость. Помогает выравнивать полоски с цифрами и определять строки на этих полосках.
• Цифровая кость. На ней расположены цифры, представляющие числа. Помогает в расчетах.
• Квадратная корневая кость. Используется для извлечения корня, а также для умножения и деления.

Чтобы было понятно, как работают кости Напьера, приведем пример. Ниже вы можете увидеть таблицу:

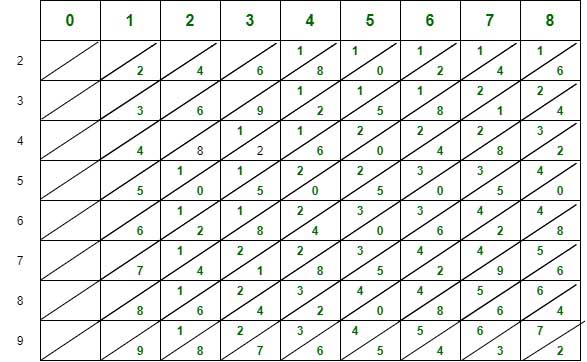
На этой таблице:

• Цифры от 0 до 8 расположены вверху столбцов.
• Цифры от 2 до 9 расположены слева от строк.
• Каждый квадрат разделен пополам диагональной линией.
• Числа над столбцами умножаются на числа слева от строк.
• В ячейках можно увидеть результат умножения чисел друг на друга.

Несмотря на то, что устройство Напьера кажется сложным и неактуальным, сегодня можно найти его готовые варианты, сделанные из дерева, металла или картона. Видимо есть эстеты от арифметики, которым нравится считать, используя оригинальные приспособления.

🏛 Таблица Пифагора

Выражение «таблица Пифагора» известно, пожалуй, каждому, и само создание таблицы умножения приписывают этому древнегреческому математику, который жил примерно в 570-495 годах до н.э.

Доказательств тому, что таблицу придумал именно Пифагор, как ни странно, не найдено. Лишь математик Никомах Герасский, живший примерно с 60 по 120 годы до н.э., говорил о том, что автором таблицы является Пифагор. Но вопрос остается открытым и по сей день.

Как бы то ни было, название «таблица Пифагора» прижилось и широко используется в обиходе в разных странах мира, например, в России, Италии и Франции. И таблицу Пифагора все мы видим на тыльной стороне обложки любой тетрадки по математике. Причинами же популярности и распространенности этой таблицы служат ее простота и удобство применения.

Вот так выглядит классическая таблица Пифагора:

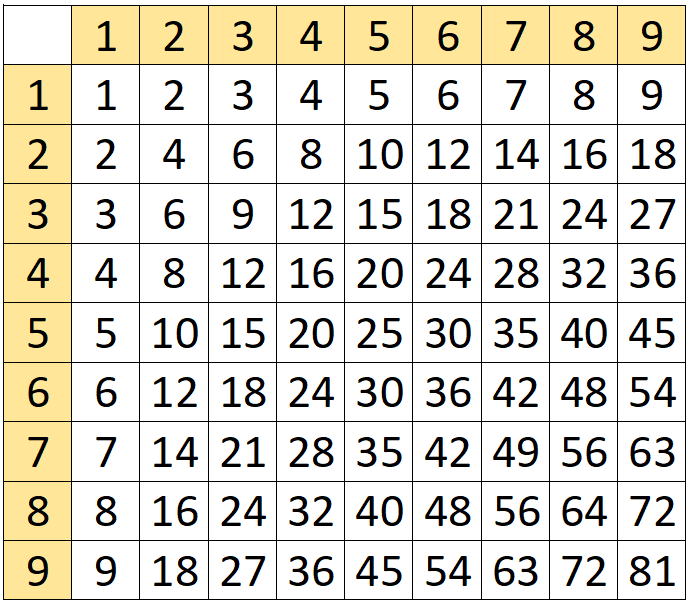
А еще есть вариант с цифрой 10 (такая таблица используется редко, т.к. умножение на 10 ни у кого не вызывает сложностей):

Существует и вариант таблицы до 12:

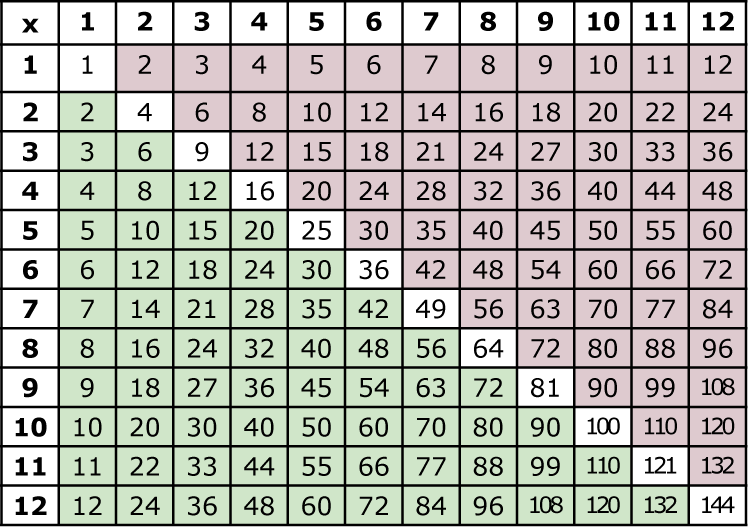
И даже до 20:

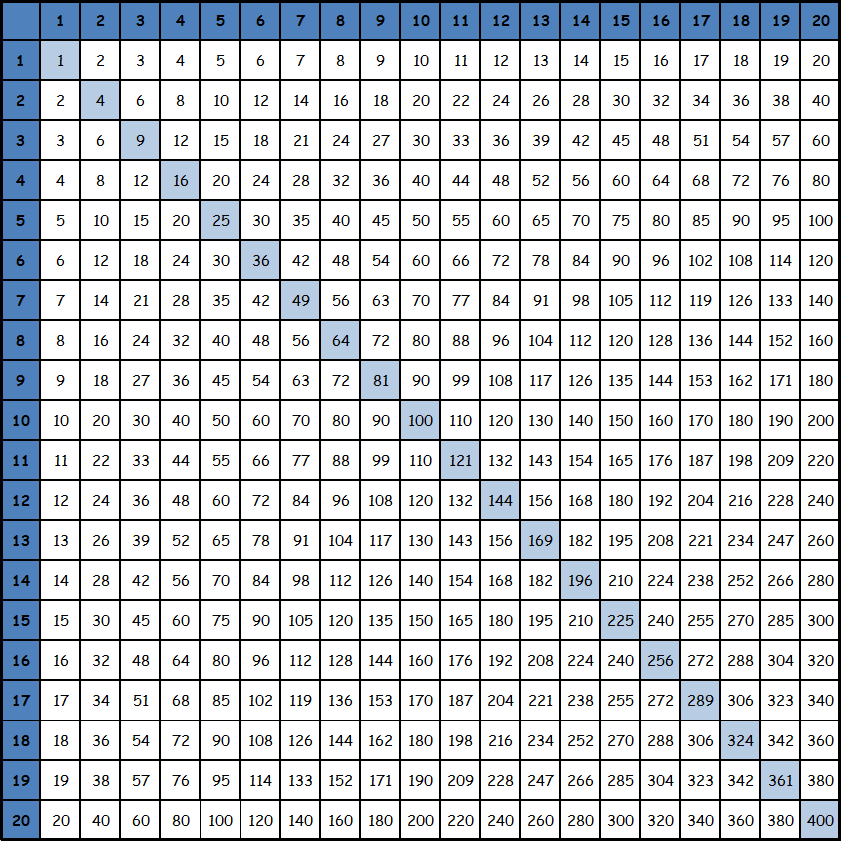
Вне зависимости от варианта в первой строке и в первом столбце находятся множители, а в ячейках – их произведения. Т.е., если вам нужно умножить 7 на 7 (6 х 7), вы выбираете в первой строке цифру 6 и в первом столбце цифру 7, а затем ищете ячейку, где они пересекаются, и получаете ответ.

Помимо прочего, таблица Пифагора интересна и сама по себе. Например, смотря на нее, можно заметить закономерности, упрощающие процесс запоминания. А еще она симметрична, и вам вовсе необязательно учить ее целиком – просто мысленно проведите диагональ (как на изображениях выше) и запомните то, что расположено под или над этой диагональю. Говоря проще, если вы знаете, сколько будет 3 х 9, вам не нужно запоминать, сколько будет 9 х 3, и т.д.

Есть и еще кое-что. Если вы выберете какое-нибудь число и проведете линию вверх, а затем в сторону множителей, вы получите прямоугольник. Количество ячеек в этом прямоугольнике будет равно числу, которое вы получите, перемножив соответствующие множители:

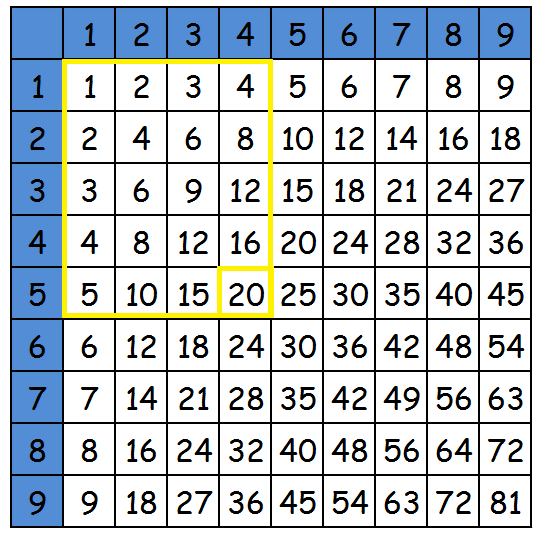
И уже отсюда можно получить геометрический смысл прямоугольника, площадь которого равна произведению его сторон. Если просто, то площадь прямоугольника – это то количество ячеек, которое заключено в прямоугольнике со сторонами с конкретными единичными значениями.

Вывод таков: таблица Пифагора не просто удобна для умножения. Суть в том, что ее в некоторой степени можно считать фундаментом математической науки. И об этом говорят даже сами математики.

🪆 Древнерусское умножение

Многие люди уверены, что существует некая древнерусская таблица умножения, однако в действительности речь идет о древнерусском умножении, которое также называют крестьянским умножением или даже древнеегипетским или эфиопским умножением. А еще оно известно под названием «умножение через удвоение и деление пополам».

На первый взгляд, данный метод может показаться непонятным, но на деле его достаточно легко освоить, и он помогает не только умножать, но и возводить в степень и рассчитывать матрицы. Алгоритм его таков:

• Записываем рядом два перемножаемых числа, которые станут заголовками двух столбцов. В третьем столбце снизу будет нарастающая сумма.
• Если в левом столбце стоит нечетное число, добавляем число из правого столбца в третий столбец. Изначально нарастающая сумма равно нулю.
• Ниже в левом столбце пишем число из заголовка, разделенное на два, и при этом отбрасываем остаток. А во втором столбце записываем число, которое равно удвоению числа в его заголовке. Учитывая, что в левом столбце стоит четное число, нарастающая сумма не увеличивается.
• Еще раз делим на два левое число и умножаем на два второе. Получая в левом столбце нечетное число, добавляем в третий столбец число из правого столбца.
• Повторяем процедуру, пока в левом столбце не останется единица (заметим, что если не довести алгоритм до конца, слева будут одни нули, а т.к. ноль является четным числом, добавлять в третий столбец будет нечего, поэтому, когда получаем слева единицу, в третьем столбце получаем ответ).
• Складываем все числа, получившиеся в третьем столбце, и у нас появляется ответ.

Вот пример такого умножения:

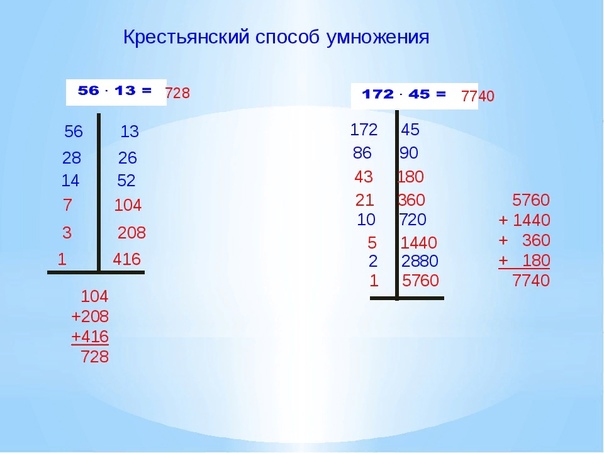
При желании вы можете проверить правильность вычислений на калькуляторе. Но мы уверяем, что способ работает безотказно. Особо интересующиеся могут найти доказательство верности этой модели в Интернете, как и примеры возведения в степень и расчета матриц.

📁 Таблица сокращенного умножения

Возможно, вы слышали о формулах сокращенного умножения. Эти формулы помогают умножать, возводить в степень числа и многочлены в сокращенном варианте – решение записывается максимально сокращенно. Также эти формулы позволяют раскладывать многочлены на множители, упрощать выражения и приводить многочлены к стандартному виду.

Как правило, формулы сокращенного умножения просто заучиваются, а потом применяются в ходе вычислений. Самих же основных формул семь:

Решая задачи, просто заменяйте буквы цифрами, переменными или целыми выражениями. А для удобства запоминания используйте аналогии. К примеру, формула квадрата суммы очень похожа на формулу квадрата разности, только знак «плюс» меняется на «минус».

Кроме перечисленных также существуют формулы возведения в квадрат суммы и разности трех, четырех и более слагаемых, разности n-ных степеней двух слагаемых и многие другие. Но они пригождаются в специфических случаях, когда требуется производить более сложные вычисления.

👐 Умножение на пальцах

Вероятно, вы удивитесь, но умножать можно и на пальцах! Для чего это нужно? Все просто: умножая на пальцах, намного легче запомнить таблицу умножения после цифры 5, а как раз цифры 6, 7, 8 и 9 вызывают у многих наибольшие затруднения, особенно у детей (учить таблицу умножения с помощью пальцев, кстати говоря, детям гораздо интереснее).

Все, что вам потребуется, – это ваши руки. Начать же лучше всего с умножения на 9 – это проще. Так что запомните обозначения своих пальцев, как показано на рисунке:

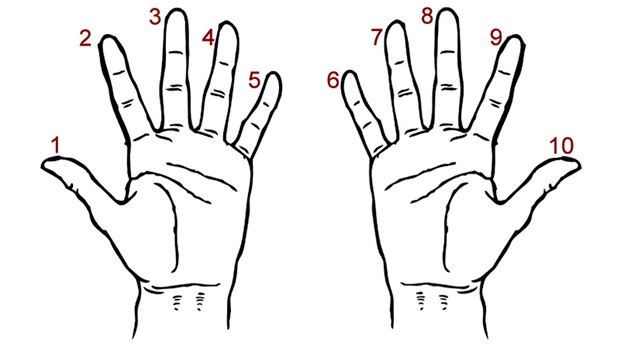
Чтобы умножить 9 на 2, загните палец №2. Количество пальцев слева обозначает десятки, а справа – единицы. Вы загнули палец №2, и у вас слева остался один палец, а справа – восемь. В итоге вы получаете 18:

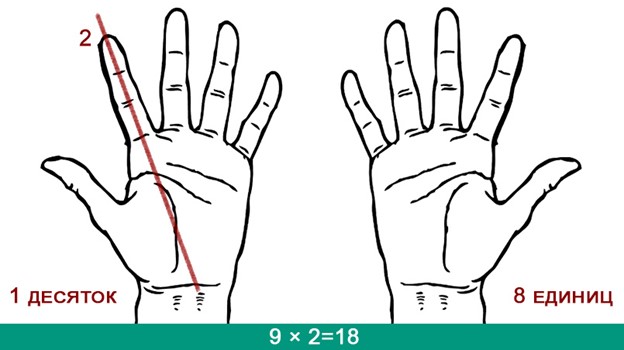
По аналогии с примером выше, если вы хотите посчитать 9 х 3, согните палец №3, и тогда слева от него останется два пальца, с справа – семь. В итоге вы получаете 27. Сгибайте пальцы дальше, и проверяйте, сколько получается.

А чтобы умножить на пальцах 6, 7 и 8, нужно пронумеровать пальцы чуть-чуть в другом порядке:

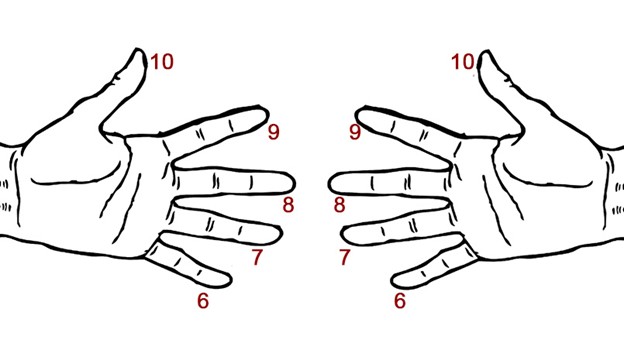
Для умножения нужно соединять пальцы соответствующих номеров. Например, чтобы умножить 8 на 7, соедините палец №8 на левой руке и палец №7 на правой (или наоборот). Снизу вы получите десятки (пальцы, которые соединены, тоже считаются), а сверху нужно умножить количество пальцев левой руки на количество пальцев правой, а затем прибавить к десяткам. В результате получается 56:

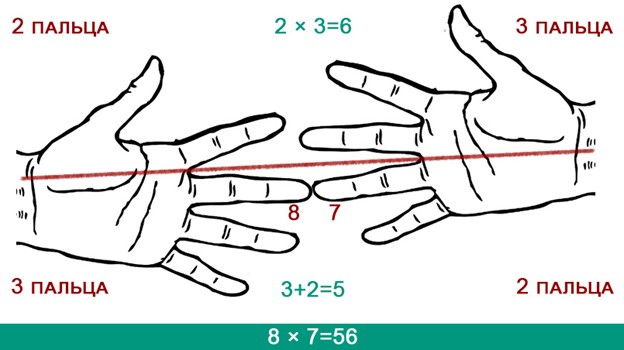
Точно так же нужно действовать и при умножении 6, 7 и 8 друг на друга. Как видите, освоить этот метод проще простого. А вашему ребенку это пойдет на пользу еще и по причине развития мелкой моторики.

🔼 Пирамида умножения

Пирамида умножения представляет собой специальную технику, помогающую запомнить таблицу умножения быстрее. В ней содержатся 36 примеров в понятном и легко запоминающемся порядке:

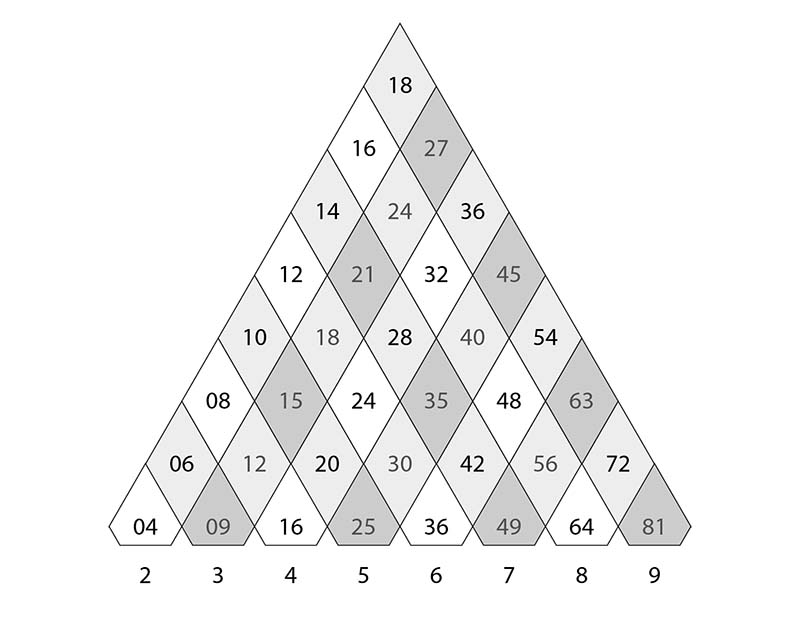
В этом варианте числовое основание расположено снизу, но есть варианты, где основание находится сбоку, и даже варианты, где числа идут сверху вниз. Но в любом случае примеры расположены так, что, начиная от основания и по направлению к вершине, с каждой степенью пирамиды количество примеров сокращается, ведь становится и меньше самих вариаций умножения.

Работать же с этой пирамидой можно, как угодно. Кто-то использует ее так, что ребенок просто заучивает ответы, а кто-то подходит более системно. Некоторые, например, делают специальные карточки в форме ячеек пирамиды, на одной стороне пишут пример, а на второй – ответ. Затем карточки перемешиваются, а ребенок должен дать правильные ответы и построить всю пирамиду.

При этом ребенок не просто запоминает, а начинает самостоятельно считать, сколько будет, к примеру, дважды пять или семью восемь. Это развивает базовые навыки счета и мотивирует использовать интеллект, а не просто зубрить, чтобы запомнить.

⚱ Арийское умножение

По мнению некоторых исследователей, та таблица умножения, которой все мы пользуемся сейчас, является лишь частью многомерной таблицы, которую некогда использовали древние арийцы. Причем, по некоторым данным, славяне начинали учить ее еще в 12-летнем возрасте.

И мы уже писали не единожды, и вы сами слышали и говорили неоднократно нечто в духе «дважды два», «пятью шесть», «семь на восемь» и т.д. А это, между прочим, как раз и есть отсылки к трем основным видам умножения «НА», «ЖДЫ» и «Ю»:

• «НА» – это привычное каждому современному человеку умножение типа 2 на 2, 3 на 5, 6 на 8 и т.д. И это умножение является двухмерным. При помощи него очень просто посчитать, к примеру, площадь. В древности умножение «НА» обозначалось точкой «⋅».
• «ЖДЫ» – это объемное и трехмерное умножение, которое обозначалось символом «х».
• «Ю» – это объемно-временное умножение, обозначавшееся символом «*».

Вот так эти три вида умножения можно представить графически:

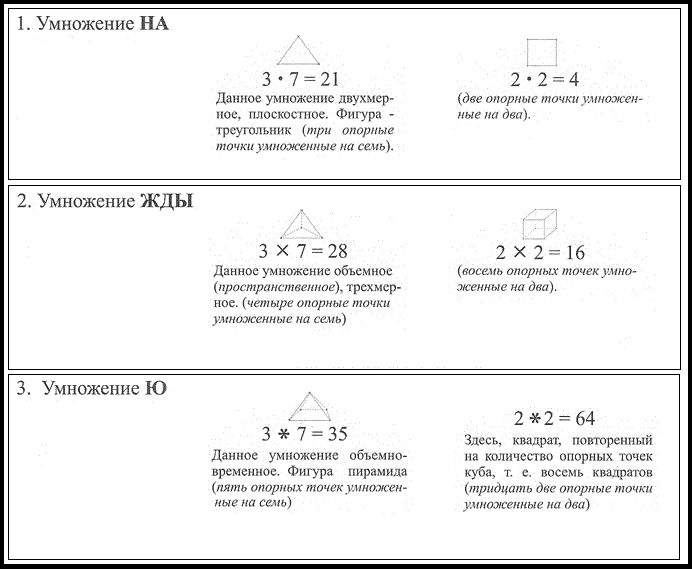
Кроме того, были и такие виды умножения, как ровное умножение, пирамидальное умножение и умножение «ПО» (вспомните 3 по 5, например).

При этом важно, что первым идет не число, как все мы привыкли, а цифра, обозначающая изначальную структуру. Следующий за ней знак помогает понять, что за фигура с основанием изначальной структуры участвует в процессе.

Давайте возьмем в качестве примера 3 х 7 = 28. Что? Нет-нет, все верно. Цифра «3» обозначает треугольник, а знак «х» обозначает пространственное умножение («ЖДЫ»). Соответственно, треугольник нужно поместить в трехмерное пространство, в котором треугольная пирамида имеет 4 опорные точки, а потому в итоге получаем 28.

Древние арийцы мыслили образами, а не просто числами, и для удобства вычислений у них существовали также и свои арифметические знаки:

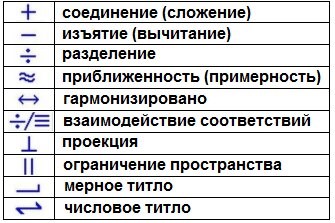
И если для простого обывателя арифметика – это лишь способ работы с числами, то для древних людей она была инструментом вычисления временных, объемных и пространственных структур. Кстати, вам знакомо выражение «Семь пядей во лбу»? Скорее всего, да, но знаете ли вы, что существует еще и древняя пядевая система мер, в которой Пядь составляет 17,78 см, а если умножить это на 7, получается Лоб, равный 124,46 см:

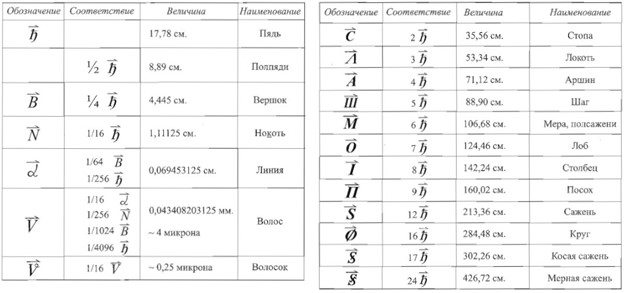
Известно и то, что в далеком прошлом даже обычный подмастерье назубок знал первые три системы умножения. Эти знания помогали людям узнать, к примеру, какое количество камня потребуется, чтобы соорудить фундамент для святилища, какой объем леса будет нужен, чтобы соорудить жилище, и т.п.

О том, какой магией могут обладать цифры, можно узнать из сравнения таблиц умножения «НА» и «ЖДЫ»:

Не менее интересна упомянутая ранее ровная система умножения:

А вот таблица пирамидального умножения:

И вишенка на торте – триадные системы умножения:

Естественно, сегодня о применении этих знаний вряд ли кто-то услышит, да и знают о них сущие единицы. Но все же, раз эти знания существуют, это говорит о том, что когда-то в древности люди вычисляли поистине невероятные вещи.

🔲 Ведический квадрат

Понятие ведического квадрата известно из индийской математики, где он является вариацией обычной таблицы умножения 9 х 9. Запись в каждой ячейке – это цифровой корень произведения заголовков столбцов и строк, и этот же корень представляет собой остаток, получаемый при делении произведения заголовков строк и столбцов на 9.

Если говорить максимально просто, то в ведическом квадрате любой результат перемноженных чисел сведен к однозначному значению от 1 до 9. Например, 7 × 6 = 42 = 6, а 8 х 6 = 48 = 12 = 3:

Это делает ведический квадрат поистине уникальным явлением. Несложно заметить, что числа от 1 до 9, которые заполняют его клетки, повторяются определенным образом. Кроме 3, 6 и 9, все остальные числа занимают по шесть клеток, числа 3 и 6 занимают по двенадцать клеток, а число 9 повторяется 21 раз.

Однако истинная работа с ведическим квадратом – это не просто умножение или деление, а произведение сложнейших вычислений из области модульной арифметики, теории категорий, абстрактной алгебры, теоретической информатики, моноидов и других алгебраических структур.

Мало того, в ведическом квадрате можно наблюдать огромное количество симметрий и геометрических узоров, некоторые из которых можно отследить в традиционном индийском и исламском искусстве (если соединить повторяющиеся числа, на выходе получится диаграмма или вполне определенный узор):

А еще этот квадрат используется в нумерологии, ведь он считается примером древнего знания, дошедшего до современного человека, в котором числа являют собой посланников космической энергии. Вот так могут выглядеть нумерологические вычисления (они вам уже знакомы):

2 × 1 = 2
2 × 2 = 4
2 × 3 = 6
2 × 4 = 8
2 × 5 = 10 = 1
2 × 6 = 12 = 3
2 × 7 = 14 = 5
2 × 8 = 16 = 7
2 × 9 = 18 = 9

Сегодня ведический квадрат не пользуется большой популярностью среди обывателей, но в Древней Индии он имел колоссальное значение. Сейчас же, как мы и сказали, он более распространен в нумерологии и, по мнению ее приверженцев, помогает улучшать жизни многих людей по всему миру.

Уверены, вы смогли заметить, что таблица умножения и содержащиеся в ней цифры – это в некоторой степени нечто магическое. Однако практическое их применение – вовсе не магия, а использование в повседневных делах, работе, учебе или бизнесе.

Вариантов таблицы умножения существует немало, и есть и те, о которых мы сегодня не рассказали, но все они говорят об одном – уметь умножать, делить и производить другие вычисления важно и нужно всем, а уж каким образом это делать – личный выбор каждого из нас.