Умножение дробей

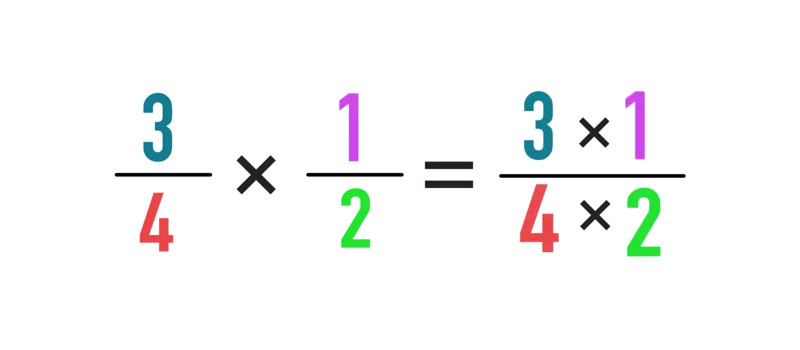
Зачем уметь работать с дробями?

Дроби используются в различных областях жизни, в том числе:

• Математика: вычисление дробных величин, операции с дробями и т.д.
• Кулинария: расчет ингредиентов для приготовления блюд.
• Финансы: вычисление процентов, деление денежных сумм на части и т.д.
• Строительство: расчет объема материалов и работ.
• Производственные процессы: расчет долей ресурсов и материалов.
• Образование: вычисление средних оценок, расчет долей в статистике.
• Медицина: расчет доз лекарств и необходимого количества компонентов.
• Геодезия: расчет длины линий и площади.
• Дизайн: расчет пропорций и размеров.
• Технологии: расчет долей энергии, памяти, дискового пространства и т.д.

И это далеко не полный список – дроби можно встретить и во многих других сферах. И в каждой из этих областей дроби используются для точного вычисления величин и удобного представления частей целого.

Кроме того, решение математических задач – прекрасный инструмент для тренировки математических навыков и отличная гимнастика для мозга. Вот лишь несколько причин, почему полезно время от времени умножать дроби и решать другие примеры:

• Это развивает логику: математические задачи требуют применения логических умений, учат связывать факты и делать выводы.
• Это улучшает память: математика требует запоминать формулы и методы решения задач, что способствует улучшению памяти.
• Это способствует креативному мышлению: некоторые математические задачи требуют применения нестандартных подходов и инициативности.
• Это улучшает мышление: математическая активность тренирует мозг на устойчивость к сложным концептам и улучшает способность к анализу и синтезу.

В целом, решение математических задач может улучшать ментальные способности и способствовать развитию мозга. Поэтому знать, как умножать дроби, и уметь это делать полезно любому человеку, а школьникам, студентам и специалистам, чья деятельность связана с математикой, особенно.

Что такое дроби и какие бывают дроби?

Дробью называют число, состоящее из одной или более равных частей единицы. Если говорить проще, то дробь обозначает часть чего-либо. К примеру, может быть один пирог, а может быть одна часть и еще несколько, например, один целый пирог и три кусочка.

Существуют дроби обыкновенные и десятичные:

Обыкновенные дроби – это дроби, состоящие из числителя, расположенного верху (делимое), и знаменателя, расположенного внизу (делитель).

Они могут быть разделены либо горизонтальной, либо косой чертой, обозначающей деление. Знаменателем отражается то, на сколько частей можно разделить целое, а числитель показывает, сколько частей имеется. Например: ¹/₂, ³/₄, ⁷/₁₀. Также следует знать, что обыкновенные дроби могут быть правильными и неправильными. В правильных дробях знаменатель больше числителя (⁶/₈, ⁹/₁₅), а в неправильных дробях легко выделить целую часть и дробную (1⁴/₅, 3²/₇). Число, которое получается, принято называть смешанной дробью.

Десятичные дроби – это дроби, в знаменателе которых расположена степень числа «10». Записываются такие дроби несколько иначе – через запятую, и имеют вид 0,7 или 0, 63 и т.п.

А еще советуем запомнить, что есть дроби:

• Числовые, т.е. состоящие из чисел. Например: ⁶/₈, 0,3 и т.п.
• Алгебраические, т.е. состоящие из переменных. Например: (a + b)(a – b). Причем здесь значение дроби будет зависеть от значений переменных.

С этими дробями и приходится работать в школе или вузе, а некоторым еще и по роду деятельности. Кстати, стоит заметить, что некоторые люди, как мы и сказали, производят математические операции с дробями ради развлечения, для тренировки своих математических способностей и/или поддержания в тонусе мозга.

Основные правила дробей

Прежде чем осваивать методы умножения дробей, необходимо усвоить несколько правил, которые могут пригодиться в самых разных ситуациях и заметно облегчить процесс решения задач. Эти правила таковы:

• Перед сложением или вычитанием дробей необходимо привести их к общему знаменателю.
• Умножение дробей производится путем умножения числителей и знаменателей.
• Деление дробей производится путем перемножения первой дроби на обратную второй дроби.
• После выполнения операций над дробями их можно сократить, деля числитель и знаменатель на их наибольший общий делитель (НОД). НОД нескольких чисел – это наибольшее натуральное число, на которое эти числа делятся без остатка.

В дополнение к этому:

• Если делитель дроби равен нулю, у дроби не будет значения.
• Дробь всегда будет равна нулю, если ее числитель равен нулю, а знаменатель не равен.
• Две дроби ^a/_bи ^c/_dбудут равными, если ad = bc.
• При умножении или делении числителя и знаменателя на одно и то же натуральное число значение дроби останется прежним.

Это основные правила работы с дробями, которые следует знать и применять при решении математических задач с использованием дробей.

Как умножать дроби?

Здесь необходимо разобрать три основных случая: когда требуется умножить дробь на дробь, когда требуется перемножить смешанные дроби и когда требуется умножить дробь на натуральное число.

Умножение дроби на дробь

Умножить дробь на дробь очень просто. Для этого нужно числитель одной дроби умножить на числитель другой, и точно так же поступить со знаменателями. В процессе также стоит подумать, можно ли дробь сократить.

Пример:

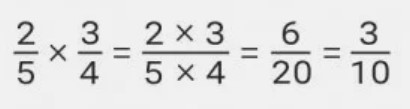
Говоря проще,числитель будет равен произведению числителей обеих дробей, а знаменатель будет равен произведению знаменателей

Это правило применимо ко всем дробям как с одинаковыми, так и с разными знаменателями. Когда дробь большая (к примеру, ²⁶/₃₇), можно попробовать сократить ее сразу, чтобы производить вычисления было проще.

В случае, когда в примере есть смешанное число, сначала нужно преобразовать его в неправильную дробь, а затем умножить предлагаемым способом, а итоговый результат вновь преобразовать в смешанное число.

Умножение десятичных дробей

Чтобы умножить десятичные дроби, нужно следовать алгоритму:

• Записать дроби столбиком и умножить, как на натуральные числа (запятые пока в расчет не берем).
• Посмотреть, сколько знаков после запятой имелось в дробях, и сложить их количество.
• Справа налево отсчитать после умножения столько цифр, сколько знаков после запятой получилось на предыдущем этапе.
• Поставить запятую перед нужным количеством цифр.

Пример:

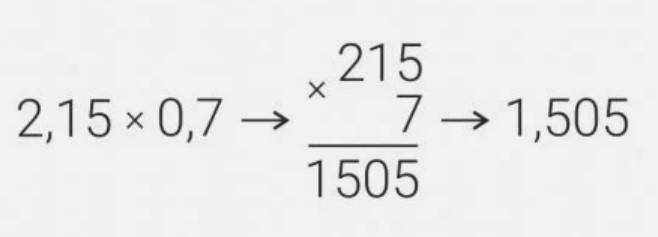
При умножении на 0,1, на 0,01, на 0, 001 и т.п. нужно переставить запятую влево на количество знаков, имеющееся после запятой в множителе. Например: 0,15 х 0,1 = 0,015 или 0,3 х 0,001 = 0,0003.

Умножение дробей на натуральные числа

При умножении дробей на натуральные числа мы снова можем столкнуться с умножением как обычных, так и десятичных дробей.

Умножение на натуральные числа обыкновенных дробей

При умножении обыкновенной дроби на натуральное число необходимо умножить лишь числитель, а знаменатель не менять. Если в результате получается неправильная дробь, нужно выделить из нее целую часть, чтобы прийти к смешанному числу.

Пример:

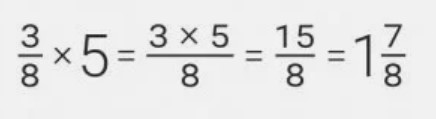
При умножении смешанного числа достаточно перевести его в неправильную дробь, а далее умножить по такой же схеме:

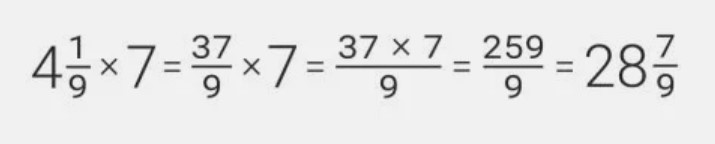
Но есть и еще один вариант. Вы можете разделить знаменатель на имеющееся натуральное число, оставив числитель без изменений. Такой способ лучше всего использовать при делении знаменателя на натуральное число без остатка.

Пример:

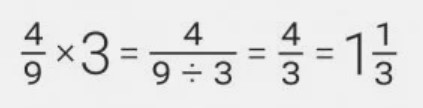
Можете попробовать решить парочку примеров двумя разными способами, и вы увидите, что ответ останется неизменным.

Умножение на натуральные числа десятичных дробей

При умножении десятичной дроби на натуральное число можно применить тот же способ, что и для умножения дроби на дробь. Сначала умножьте числа столбиком, а затем отсчитайте количество цифр, имеющееся после запятой в десятичной дроби. В этом месте должна стоять запятая.

Пример:

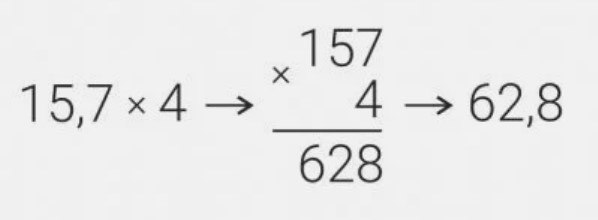
Когда требуется умножить десятичную дробь на 10, на 100, на 1000 и т.п., нужно просто переместить запятую вправо на количество знаков равное количеству нулей после единицы. К примеру: 0,025 х 10 = 0,25 или 0,025 х 100 = 2,5.

Как вы заметили, умножать дроби очень просто, несмотря на то что изначально примеры с дробями могут пугать и вводить в ступор. Немного попрактиковавшись, вы научитесь решать массу математических задач и выполнять вычисления, требующие дробных ответов, в различных областях, таких как финансы, наука, инженерия и, конечно же, математика.