Японский метод умножения с кругами

Среди разных способов умножения чисел существует очень интересный и удобный метод, изобретенный в Японии, который основан на рисовании кругов и дальнейшем подсчете их секторов. Порядок действий чем-то похож на китайский способ, но всё же в японском имеются свои черты, имеющие некоторые отличия.

Суть японской системы умножения

Давайте попытаемся разобрать это на примере:

Чтобы умножить 23 × 45, нам нужно изобразить число 23, поэтому нарисуем круги: два «двойных» для десятков и два «тройных» для единиц.

Почему мы рисуем именно два круга каждого вида?

Причина заключается в том, что число 23 мы умножаем на двухзначный множитель 45. Здесь мы будем изображать каждый из множителей сверху вниз и слева направо, также, как и в китайском способе.

Далее переходим к числу 45, которое нам нужно будет тоже изобразить.

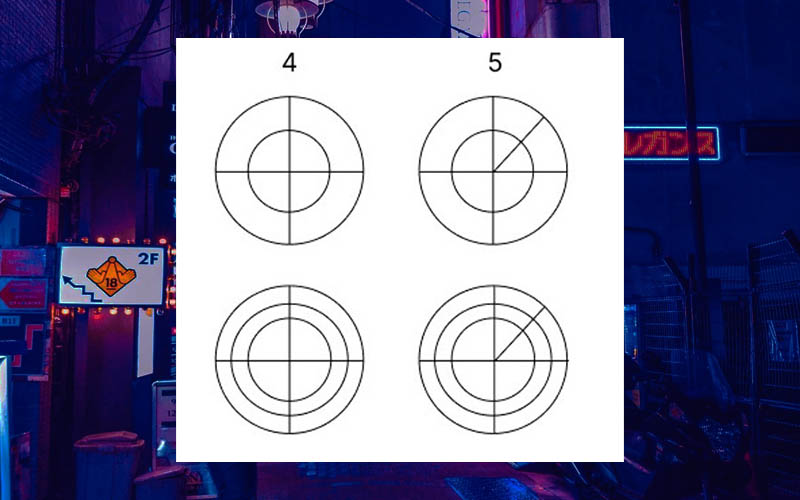
Для этого, начиная с верхнего левого угла и двигаясь по столбикам, нам необходимо разделить круги на четыре и на пять частей (45) так же, как показано на рисунке.

При этом сектора кругов не должны быть равными по размеру. Их можно примерно разделить и на глаз, главное здесь – количество самих частей.

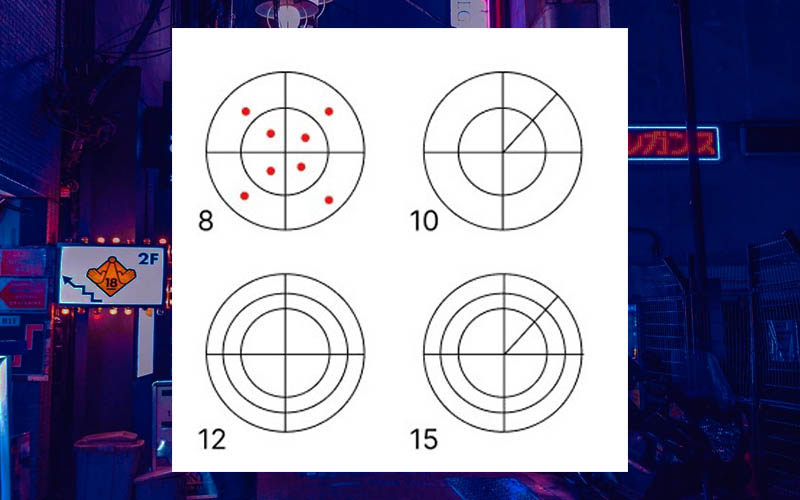
После этого нам нужно подсчитать количество секторов, образовавшихся в результате деления этих колец. Для большего удобства мы можем ставить точку в каждом секторе ручкой.

Далее эти круги снова делим на группы, точно также, как в китайском способе: нижний правый угол – это единицы, диагональ – идут десятки, и верхний левый угол – это сотни.

В итоге в результате такого умножения получается 15 единиц, 22 десятка и 8 сотен, то есть, нам снова нужно будет применить правило перехода через десяток.

Продолжаем начинать с единиц.

От 15 будем оставлять пятерку и «перебросим» единицу в следующий разряд.

Далее в разряде десятков получилось 22 + 1 = 23 десятка, мы оставим тройку, а двойку снова «перебросим» в старший разряд.

У нас стало сотен 8 + 2 = 10, другими словами, десять сотен – это тысяча.

Формируем ответ:

Тысяча + три десятка + пять единиц и в результате имеем 23 × 45 = 1035.

Японский способ очень удобен, в первую очередь, своей наглядностью. Поскольку все изображено на бумаге, значит не требуется в голове производить одновременно множество арифметических действий. Такой способ отлично подходит для умножения даже тем, кто не знает таблицу.

Тем не менее данный метод имеет некоторые минусы.

Например, при этом умножении не очень удобно вычислять произведения четырехзначных, а также более крупных чисел, потому что запись становится очень громоздкой и в ней можно легко запутаться.

Поэтому, когда речь идет о больших числах, лучше находить произведение таких больших чисел привычным нам всем «столбиком».

Когда требуется умножить разные числа, например двузначные на трехзначные, тогда проще всего воспользоваться именно японским методом с кругами, в отличие, например, от китайского способа с линиями. Тогда таблица из кругов будет иметь не квадратную форму, а прямоугольную, например, 2 × 3, но суть всех действий останется неизменной.