Формулы сокращенного умножения
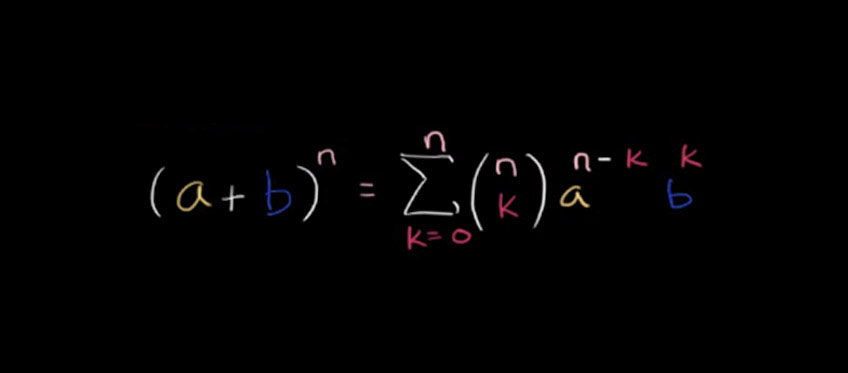
Зачем нужны формулы сокращенного умножения?
Формулы сокращенного умножения (ФСУ) используются для упрощения многочленов в алгебре. Они позволяют уменьшить количество слагаемых в многочлене и представить его в более компактной форме. Например, с использованием формулы сокращенного умножения можно умножить (x + 2)(x + 3) и получить x2 + 5x + 6 вместо (x2 + 5x + 6) + (x2 + x + 6).
ФСУ позволяют решать такие задачи, как:
- Умножение многочленов.
- Решение уравнений и неравенств многочленов.
- Решение геометрических задач.
- Расчет коэффициентов многочленов.
- Решение задач в математической статистике.
Также ФСУ могут применяться и в других областях математики, таких как линейная алгебра, комбинаторика, математическая физика и т.д.
Кроме того, ФСУ могут быть полезны в ряде случаев и для обычного человека:
- Решение домашних заданий. Например, для выполнения заданий по математике, когда нужно решать задачи по многочленам.
- Решение жизненных задач. Например, для расчета площади и объема тел с использованием многочленов.
- Решение кроссвордов и головоломок. Например, для ответов на вопросы и решения головоломок, которые связаны с математикой.
- Решение задач в свободное время. Формулы сокращенного умножения могут быть интересным развлечением. Например, в свободное время вы можете решать те же математические головоломки или развивать математические навыки.
Начало формы
В целом, знание формул сокращенного умножения позволяет человеку не только справляться с математическими заданиями, но и развивать свой интеллект и поддерживать в тонусе мозг, что помогает продлить его здоровье и предупредить возникновение различных возрастных изменений, в том числе и очень опасных.
Какие есть формулы сокращенного умножения?
Вообще, есть несколько основных ФСУ и ряд дополнительных. Основные используются чаще всего, а выделить среди них можно следующие:
- Квадрат суммы: (a + b)² = a² + 2ab + b²
- Квадрат разности: (a – b)² = a² – 2ab + b²
- Разность квадратов: (a – b)(a + b) = a² – b²
- Сумма кубов: (a + b)(a² – ab + b²) = a³ + b³
- Разность кубов: (a – b)(a² + ab + b²) = a³ – b³
- Куб суммы: (a + b)³ = a³ + 3a²b + 3ab² + b³
- Куб разности: (a – b)³ = a³ – 3a²b + 3ab² – b³
Кстати, если поменять местами левую и правую части формул, мы получим формулы разложения на множители, а именно:
- Квадрат суммы: a² + 2ab + b² = (a + b)²
- Квадрат разности: a² – 2ab + b² = (a – b)²
- Разность квадратов: a² – b² = (a – b)(a + b)
- Сумма кубов: a³ + b³ = (a + b)(a² – ab + b²)
- Разность кубов: a³ – b³ = (a – b)(a² + ab + b²)
- Куб суммы: a³ + 3a²b + 3ab² + b³ = (a + b)³
- Куб разности: a³ – 3a²b + 3ab² – b³ = (a – b)³
Эта обратная запись ФСУ отлично годится, чтобы раскладывать на множители многочлены, сокращать алгебраические дроби и решать самые разные примеры.
И при всем этом очень важно раз и навсегда запомнить, что:
- (a + b)2 ≠ a2+ b2
- (a – b)2 ≠ a2– b2
Эта ошибка (когда люди ставят знак равенства между данными частями уравнений) встречается очень часто и приводит к многочисленным неправильным решениям.
Что же касается непосредственно ФСУ, то обычно в школе учителя просят учеников все эти формулы запомнить, однако их достаточно легко получить. Для этого нужно просто раскрыть скобки с помощью закона распределения (распределительного закона).
Распределительный закон
Распределительный закон в математике – это формальное определение для свойства алгебраических операций, которое говорит о том, что произведение двух скобок равно сумме произведений каждого элемента в первой скобке с каждым элементом во второй скобке. Если проще, то можно умножать на число либо всю сумму, либо отдельно каждое слагаемое, и результат будет один и тот же.
Распределительный закон может быть описан формулой:
(a+b)c = ac + bc
А еще можете запомнить другие формулы распределительного закона:
- ab + ac = a(b + c)
- a(b + c) = ab + ac
- ab – ac = a(b – c)
- ab + ac + ad + … = a (b + c + d + …)
Давайте посмотрим на действие этого закона на примере.
Как мы помним, распределительный закон можно применить к следующему выражению:
a(b + c) = ab + ac
Здесь мы распределяем множитель «а» над слагаемыми «b» и «c» внутри скобок. Это означает, что мы умножаем «а» на «b» и «а» на «c» и получаем ab и ac соответственно. Например:
3(4 + 5) = 3 × 4 + 3 × 5 = 12 + 15 = 27
Также можно использовать распределительный закон наоборот, т.е. (a + b)c = ac + bc, и тогда мы получим:
(3 + 2)5 = 3 × 5 + 2 × 5 = 15 + 10 = 25
В обоих случаях результат совпадает, даже если мы распределили умножение до или после сложения.
Распределительный закон может быть применен и к сложным выражениям с несколькими скобками и сложными множителями. Например:
a(b + c + d) – e(f + g) = a(b + c + d) – ef – eg = ab + ac + ad – ef – eg
Здесь мы распределяем множитель «а» над слагаемыми «b», «c» и «d» внутри первых скобок, а множитель «e» над слагаемыми «f» и «g» внутри вторых скобок. Это означает, что мы умножаем «a» Начало формы
на «b», «a» на «c» и «a» на «d» и получаем ab, ac и ad соответственно. Также мы умножаем «e» на «f» и «e» на «g» и получаем ef и eg соответственно. Например:
2(3 + 4 + 5) – 3(2 + 1) = 2 × 3 + 2 × 4 + 2 × 5 – 3 × 2 – 3 × 1 = 6 + 8 + 10 – 6 – 3 = 15
В этом примере сначала мы раскрываем скобки и применяем распределительный закон, а затем складываем и вычитаем соответствующие члены, получая результат.
Важно отметить, что применение распределительного закона может помочь упростить и ускорить решение математических задач, но необходимо быть внимательными и тщательно проверять правильность решения, особенно в сложных выражениях.
Как запомнить формулы сокращенного умножения?
Самый простой способ запомнить ФСУ – это выучить их названия. Например, у нас есть формула (a + b)2, т.е. квадрат скобок, а в скобках у нас сумма, и это значит, что данное выражение называется квадратом суммы (точно так же, как квадрат разности, если в скобках стоит знак «–»). По аналогии, (a + b)3 и (a – b)3 будут называться кубом суммы и кубом разности.
Если же мы имеем выражение a2 – b2, где оба выражения в квадрате, это будет разностью квадратов. И точно так же можно запомнить, что такое разность и сумма кубов и т.д.
Но как же запомнить сами формулы? Здесь на помощь приходят механическая память и несколько секретов запоминания. Например, нам нужно запомнить квадрат суммы (a + b)² = a² + 2ab + b². Смотреть на формулу и стараться ее «сфотографировать» – не очень эффективная стратегия. Лучше всего выучить формулу в ее словесной формулировке, а звучит она так:
- Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
Словесные формулировки многократно улучшают запоминание ФСУ и пригождаются в самых разных ситуациях, когда приходится эти самые формулы вспоминать. Поэтому запомните и формулировки других формул:
- Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
- Разность квадратов двух выражений равна произведению их разности и их суммы.
- Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
- Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.
- Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
- Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.
Запомнить эти формулировки при должном усердии достаточно просто. Но не возникло ли у вас сомнений в том, что все эти формулы верны? Если сомнения возникли, это вполне нормальное явление, ведь сомневаться всегда полезно. И несмотря на то, что данные ФСУ используются людьми уже много лет, давайте все же посмотрим на их доказательство.
Доказательство формул сокращенного умножения
Доказательство ФСУ мы рассмотрим на примере формулы разности квадратов.
Как мы помним, разность квадратов двух чисел a и b равна произведению их разности и их суммы, т.е. a2 – b2 = (a – b)(a + b).
Говоря другими словами, произведение суммы a и b на их разность равно разности их квадратов, т.е. (a – b )(a + b) = a2 – b2.
При этом важно помнить, что разность квадратов не равна квадрату разности, т.е. a2 – b2 ≠ (a – b)2.
Поэтому давайте докажем, что a2 – b2 = (a – b)(a + b).
Начало формы
С помощью искусственного метода прибавим и отнимем одно и тоже ab:
+ ab – ab = 0, т.е. a2 – b2 = a2 – b2 + ab – ab
Если сгруппировать другим образом, мы получим:
a2 – b2 + ab – ab = a2 – ab + ab – b2
Продолжая группировать, получаем:
a2 – ab – b2 + ab = (a2 – ab) + (ab – b2)
Теперь выносим общие множители за скобки и получаем:
(a2 – ab) + (ab – b2) = a(a – b) + b(a – b)
Выносим за скобки (a – b) и получаем:
a(a – b) + b(a – b) = (a – b)(a + b)
И результатом доказательства является:
a2 – b2 = (a – b)(a + b)
А чтобы доказать формулу в обратную сторону, т.е. что (a – b)(a + b) = a2 – b2, раскрываем скобки и получаем:
(a – b)(a + b) = aa + ab – ba – bb = a2 – b2.
Остальные ФСУ можно доказать аналогичным методом.
А еще вы наверняка помните, что мы говорили о дополнительных формулах сокращенного умножения. О них стоит сказать чуть подробнее.
Дополнительные формулы сокращенного умножения
Есть три основные дополнительные ФСУ – это бином Ньютона, формула возведения в квадрат суммы трех, четырех и более слагаемых, а также формула разности n-ых степеней двух слагаемых. Коротко о каждой из них.
Бином Ньютона
Бином Ньютона – это формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Выглядит она следующим образом:
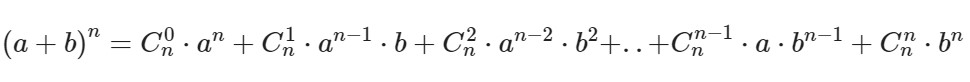
Ck в степени n – это биноминальные коэффициенты, стоящие в строке под номером n в треугольнике Паскаля. Вычисляются эти коэффициенты по формуле:
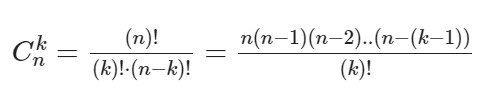
Иначе говоря, ФСУ для квадрата и куба разности и суммы являются частными случаями формулы бинома Ньютона при n=2 и n=3 соответственно.
Однако может быть так, что слагаемых в сумме, которую нужно возвести в степень, больше, чем два. В таком случае подойдет формула квадрата суммы трех, четырех и более слагаемых.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Как и было сказано, формула возведения в квадрат суммы трех, четырех и более слагаемых нужна, когда слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
Выглядит она так:
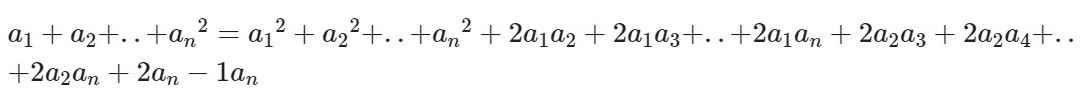
Читать и запоминать эту формулу нужно следующим образом: квадрат суммы n слагаемых равен сумме квадратов всех слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
И последняя формула – это формула разности n-ых степеней двух слагаемых, выглядящая вот так:
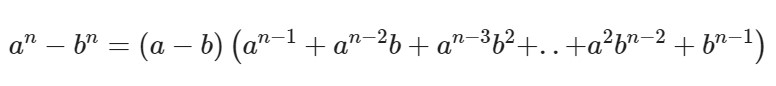
Как правило, данную формулу разделяют на две отдельные: для четных и нечетных степеней.
Формула для четных показателей 2m:
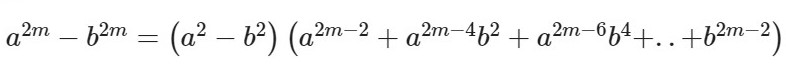
Формула для нечетных показателей 2m + 1:
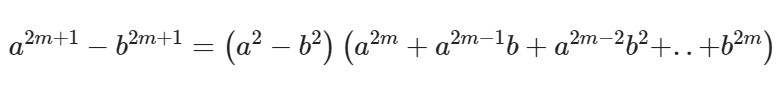
Несложно догадаться, что ФСУ разности квадратов и кубов являются частными случаями данной формулы при n=2 и n=3 соответственно. А для разности кубов b заменяется на –b.
Рассмотренные нами ФСУ и дополнительные ФСУ обязательно помогут вам быстрее справляться с математическими задачами и занимать свой мозг полезной деятельностью.
❓Вопросы и ответы
И напоследок несколько ответов на часто задаваемые вопросы.
Для чего нужны формулы сокращенного умножения?
Формулы сокращенного умножения нужны, чтобы упростить и ускорить вычисления, а также для улучшения наглядности и понимания математических выражений.
В настоящее время ФСУ широко используются в образовании и науке, а также в практической жизни. Они применяются в различных областях, таких как математика, физика, химия и инженерия, плюс могут применяться к решению различных задач, например, в области финансов, менеджмента и исследования данных.
Как появились формулы сокращенного умножения?
Формулы сокращенного умножения появились в результате исследований математиков в области алгебры и арифметики и основаны на использовании их свойств, таких как коммутативность, ассоциативность и дистрибутивность.
Если обратиться к истории, можно узнать, что такими формулами пользовались еще в Древнем Вавилоне и Древнем Египте. Первым же, кто доказал математическую закономерность квадрата суммы, был древнегреческий ученый Евклид, живший в III веке до н.э. А на общепринятом языке математические формулы были обоснованы Исааком Ньютоном.
Сколько всего формул сокращенного умножения?
Не существует точного количества формул сокращенного умножения, т.к. их можно создавать неограниченное количество. Но в основном изучают и используют семь основных формул. Это квадрат суммы, квадрат разности, разность квадратов, сумма кубов, разность кубов, куб суммы и куб разности. Также распространено применения трех дополнительных ФСУ, таких как бином Ньютона, формула возведения в квадрат суммы трех, четырех и более слагаемых и формула разности n-ых степеней двух слагаемых.
Почему формулы сокращенного умножения изучают на алгебре в 7 классе?
Формулы сокращенного умножения изучаются на алгебре в 7 классе, потому что именно на этом этапе школьники знакомятся с понятием многочлена и действиям с ним. Кроме того, ФСУ являются важным и основным инструментом для решения математических задач и упрощения вычислений.
Формулы помогают ученикам развить навыки в решении простых задач, а также дают им навыки для решения более сложных задач в будущем, что в перспективе способно помочь молодым людям в их дальнейшем обучении и карьере.
Можно ли не использовать формулы сокращенного умножения?
Конечно, при решении математических задач можно и не использовать формулы сокращенного умножения. Однако без них процесс решения может оказаться очень трудоемким и долгим. ФСУ же заметно упрощают его и помогают справляться с заданиями намного быстрее.
Помимо прочего, ФСУ входят в обязательную школьную программу, вследствие чего преподаватели часто требуют от учеников, во-первых, знать эти формулы наизусть, а во-вторых, решать задания именно с их помощью.